
- May -akda Miles Stephen [email protected].
- Public 2023-12-15 23:41.
- Huling binago 2025-06-01 05:06.
Ang maliit na teorama ni Fermat nagsasaad na kung ang p ay isang prime number, kung gayon para sa anumang integer a, ang numerong a p - ang a ay isang integer multiple ng p. ap ≡ a (mod p). Espesyal na Kaso: Kung ang a ay hindi nahahati sa p, Ang maliit na teorama ni Fermat ay katumbas ng pahayag na a p-1-1 ay isang integer multiple ng p.
Sa ganitong paraan, paano mo mapapatunayan ang maliit na teorama ni Fermat?
Hayaan ang p ay isang prime at isang anumang integer, pagkatapos ay ap = a (mod p). Patunay. Ang resulta ay trival (magkabilang panig ay sero) kung p divides a. Kung hindi hinahati ng p ang a, kailangan lang nating i-multiply ang congruence sa Ang Little Theorem ni Fermat sa pamamagitan ng isang upang makumpleto ang patunay.
Alamin din, ano ang solusyon sa Huling Teorem ni Fermat? Solusyon para sa Ang Huling Teorama ni Fermat . Ang Huling Teorama ni Fermat (FLT), (1637), ay nagsasaad na kung ang n ay isang integer na mas malaki kaysa sa 2, imposibleng makahanap ng tatlong natural na numerong x, y at z kung saan ang pagkakapantay-pantay ay natutugunan bilang (x, y)>0 sa xn+yn =zn.
Kung isasaalang-alang ito, bakit mahalaga ang maliit na teorama ni Fermat?
Ang maliit na teorama ni Fermat ay isang pundamental teorama sa elementarya na teorya ng numero, na tumutulong sa pagkalkula ng mga kapangyarihan ng mga integer na modulo prime na numero. Ito ay isang espesyal na kaso ng Euler's teorama , at ay mahalaga sa mga aplikasyon ng teorya ng elementarya, kabilang ang primality testing at public-key cryptography.
Ano ang ibig sabihin ng teorama ni Euler?
Teorem ni Euler . Ang paglalahat ng Fermat's teorama ay kilala bilang Ang teorama ni Euler . Sa pangkalahatan, Ang teorama ni Euler nagsasaad na, “kung ang p at q ay relatibong prime, kung gayon”, kung saan ang φ ay kay Euler totient function para sa mga integer. Ibig sabihin, ay ang bilang ng mga di-negatibong numero na mas mababa sa q at medyo prime sa q.
Inirerekumendang:
Paano ko gagawin ang isang ibabaw sa isang polyline sa AutoCAD?
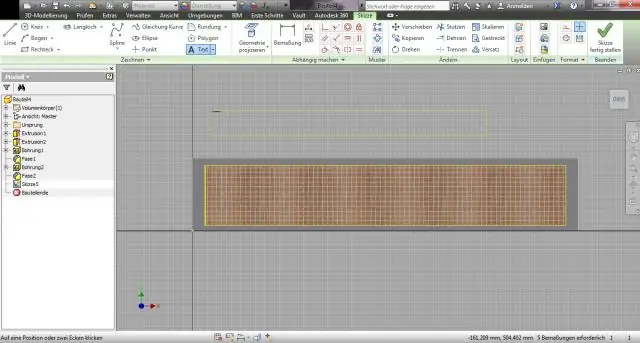
Re: I-convert ang surface boundary sa polyline I-on ang iyong border sa loob ng iyong surface style, piliin ang surface at sa loob ng contextual ribbon ay mayroong icon na extract objects, pagkatapos ay may lalabas na dialogue na nagtatanong kung ano ang gusto mong i-extract. Alisan ng check ang lahat maliban sa hangganan, pindutin ang ok
Paano mo gagawin ang pinakamahusay na pagsabog ng bulkan?

Baking Soda at Vinegar Volcano Plastic cup (Sinubukan namin ang isang bote ng tubig, ngunit ang plastic cupworked much better) Tubig. 3-4 Tbs of baking soda man lang (kadalasan naming ginagawa ang 4-6 na ginagawang mas mabula at 2-3 eruptions) 1 tsp ng dish soap. 1/2 oz hanggang 2 oz ng Washable Paint, depende sa intensity ng ninanais na kulay
Paano mo gagawin ang isang Punnett square na may maraming alleles?
Mahalagang sundin mo ang mga kinakailangang hakbang! Una kailangan mong itatag ang iyong parental cross, o P1. Susunod na kailangan mong gumawa ng 16 square Punnett Square para sa iyong 2 katangian na gusto mong i-cross. Ang susunod na hakbang ay upang matukoy ang mga genotype ng dalawang magulang at magtalaga sa kanila ng mga titik upang kumatawan sa mga alleles
Paano mo gagawin ang isang minus sum sa Excel?
Tandaan: Walang SUBTRACT function sa Excel. Gamitin ang function na SUM at i-convert ang anumang mga numero na gusto mong ibawas sa kanilang mga negatibong halaga. Halimbawa, ang SUM(100,-32,15,-6) ay nagbabalik ng 77
Paano mo gagawin ang Excel na kalkulahin ang mga formula?
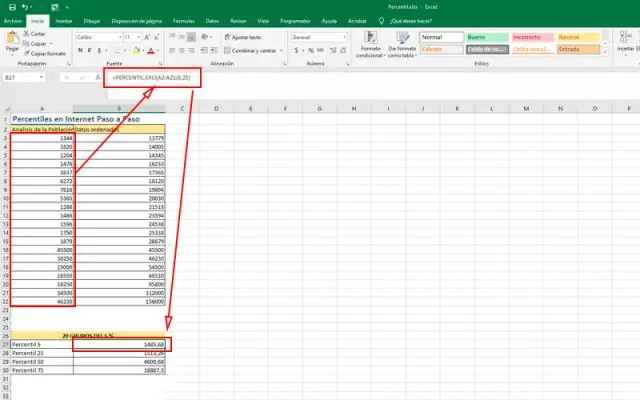
Paglikha ng mga simpleng formula Piliin ang cell kung saan lalabas ang sagot (B4, halimbawa). Pinili ang cell B4. I-type ang equals sign (=). I-type ang formula na gusto mong kalkulahin ng Excel (75/250, halimbawa). Paglalagay ng formula saB4. Pindutin ang enter. Ang formula ay kakalkulahin, at ang halaga ay ipapakita sa cell. Resulta sa B4
