- May -akda Miles Stephen [email protected].
- Public 2023-12-15 23:41.
- Huling binago 2025-01-22 17:12.
Ang una, na nagpapakita na ang limitasyon AY umiral , ay kung ang graph ay may butas sa linya, na may punto para sa na halaga ng x sa ibang halaga ng y. Kung nangyayari ito, pagkatapos ay ang umiiral ang limitasyon , bagama't mayroon itong ibang halaga para sa function kaysa sa halaga para sa limitasyon.
Gayundin, ano ang limitasyon sa isang graph?
Isang one-sided limitasyon ay ang halaga na nilalapitan ng function habang ang mga x-values ay lumalapit sa limitasyon mula sa *isang tabi lamang*. Ang isang panig *kanan* limitasyon ng f sa x=0 ay 1, at ang one-sided *kaliwa* limitasyon sa x=0 ay -1.
Katulad nito, ano ang pormal na kahulugan ng isang limitasyon? Pormal na kahulugan ng mga limitasyon Bahagi 3: ang kahulugan . Tungkol sa Transcript. Ang epsilon-delta kahulugan ng mga limitasyon sinasabi na ang limitasyon ng f(x) sa x=c ay L kung para sa alinmang ε>0 mayroong δ>0 na kung ang distansya ng x mula sa c ay mas mababa sa δ, kung gayon ang distansya ng f(x) mula sa L ay mas mababa sa ε.
Kung gayon, maaari bang maging limitasyon ang 0?
Upang masabi ang limitasyon umiiral, ang pag-andar ay kailangang lapitan ang parehong halaga anuman ang direksyon ng x nanggaling (Tintukoy namin ito bilang kalayaan sa direksyon). Dahil hindi iyon totoo para sa function na ito habang papalapit ang x 0 , ang ginagawa ng limitasyon hindi umiiral.
Ano ang layunin ng mga limitasyon?
Sa matematika, a limitasyon ay ang halaga na a function (o sequence) "lumalapit" habang ang input (o index) ay "lumalapit" sa ilang halaga. Mga limitasyon ay mahalaga sa calculus (at mathematical analysis sa pangkalahatan) at ginagamit upang tukuyin ang continuity, derivatives, at integrals.
Inirerekumendang:
Paano mo malalaman kung ang isang polynomial graph ay positibo o negatibo?
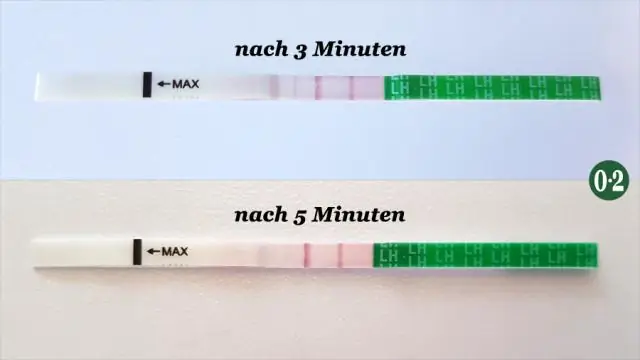
Kung ang degree ay kakaiba at ang nangungunang koepisyent ay positibo, ang kaliwang bahagi ng graph ay tumuturo pababa at ang kanang bahagi ay tumuturo pataas. Kung ang degree ay kakaiba at ang nangungunang coefficient ay negatibo, ang kaliwang bahagi ng graph ay tumuturo pataas at ang kanang bahagi ay tumuturo pababa
Paano mo malalaman kung kailan dapat i-stretch o paliitin ang isang graph?

Mga Pangunahing Takeaway Kapag sa alinman sa f(x) o x ay na-multiply sa isang numero, ang mga function ay maaaring "mag-unat" o "lumiit" nang patayo o pahalang, ayon sa pagkakabanggit, kapag na-graph. Sa pangkalahatan, ang isang patayong kahabaan ay ibinibigay ng equation na y=bf(x) y = b f (x). Sa pangkalahatan, ang isang pahalang na kahabaan ay ibinibigay ng equation na y=f(cx) y = f (c x)
Paano mo malalaman kung ano ang i-shade sa isang graph?
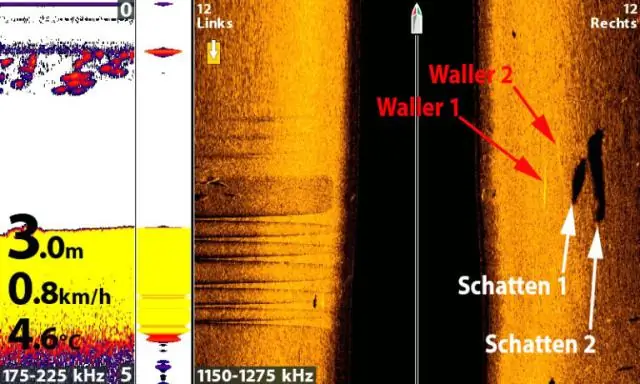
Paano Mag-graph ng Linear Inequality Muling ayusin ang equation upang ang 'y' ay nasa kaliwa at lahat ng iba pa sa kanan. I-plot ang linyang 'y=' (gawin itong solidong linya para sa y≤ o y≥, at putol-putol na linya para sa y) I-shade sa itaas ng linya para sa 'mas malaki kaysa' (y> o y≥) o sa ibaba ng linya para sa isang 'mas mababa sa' (y< o y≤)
Paano malalaman ng isang geologist kung ang isang fold ay isang syncline at isang anticline?

Geologic Structures (Bahagi 5) Ang Anticlines ay mga fold kung saan ang bawat kalahati ng fold ay lumulubog palayo sa crest. Ang mga syncline ay mga fold kung saan ang bawat kalahati ng fold ay lumulubog patungo sa labangan ng fold. Maaalala mo ang pagkakaiba sa pamamagitan ng pagpuna na ang mga anticline ay bumubuo ng isang "A" na hugis, at ang mga syncline ay bumubuo sa ilalim ng isang "S."
Paano mo malalaman kung ang isang piecewise graph ay isang function?

Paano Malalaman kung ang Piecewise Function ay Continuous o Hindi Continuous. Upang malaman kung ang isang piecewise graph ay tuluy-tuloy o hindi tuloy-tuloy, maaari mong tingnan ang mga boundary point at tingnan kung ang y point ay pareho sa bawat isa sa kanila.(Kung ang mga y ay magkaiba, magkakaroon ng "jump" sa graph !)
