
- May -akda Miles Stephen [email protected].
- Public 2023-12-15 23:41.
- Huling binago 2025-01-22 17:12.
Isang unang order differential equation ay eksakto kung ito ay may conserved na dami. Halimbawa, mapaghihiwalay na equation Palagi eksakto , dahil sa kahulugan ang mga ito ay nasa anyong: M(y)y + N(t)=0, kaya ang ϕ(t, y) = A(y) + B(t) ay isang conserved na dami.
Higit pa rito, mapaghihiwalay ba ang isang differential equation?
Mga Equation na Nahihiwalay . Isang unang order differential equation y'=f(x, y) ay tinatawag na a separable equation kung ang function na f(x, y) ay maisasalik sa produkto ng dalawang function ng x at y: f(x, y)=p(x)h(y), kung saan ang p(x) at h(y) ay tuluy-tuloy na pag-andar.
Gayundin, paano mo isasama ang dy dx xy? Hakbang 1 Paghiwalayin ang mga variable sa pamamagitan ng paglipat ng lahat ng y terms sa isang bahagi ng equation at lahat ng x terms sa kabilang panig:
- I-multiply ang magkabilang panig sa dx:dy = (1/y) dx. I-multiply ang magkabilang panig sa y: y dy = dx.
- Ilagay ang integral sign sa harap:∫ y dy = ∫ dx. Pagsamahin ang bawat panig: (y2)/2 = x + C.
- I-multiply ang magkabilang panig sa 2: y2 = 2(x + C)
Sa ganitong paraan, kapag ang isang differential equation ay eksakto?
Ang binigay eksakto ang equation dahil ang mga partial derivatives ay pareho: ∂Q∂x=∂∂x(x2+3y2)=2x, ∂P∂y=∂∂y(2xy)=2x.
Ano ang ibig sabihin ng dy dx?
Sa pamamagitan ng d/dx ang ibig nating sabihin ay mayroong function na maiiba; Ang d/dx ng isang bagay ay nangangahulugan na ang "isang bagay" ay dapat ibahin sa paggalang sa x. dy/dx ibig sabihin ay "ibahin ang y na may paggalang sa x" bilang dy/dx pareho ang ibig sabihin ng d/dx(y).
Inirerekumendang:
Ano ang differential weathering at erosion?

Ang differential weathering at differential erosion ay tumutukoy sa matitigas, lumalaban na mga bato at mineral na bumabagal at mas mabagal ang pagguho kaysa sa mas malambot, hindi gaanong lumalaban na mga bato at mineral. Ang batong ipinapakita sa ibaba ay isang mapanghimasok na igneous rock (gabbro?) na may dalawang magkasalubong na granite dike. Ang mga dike ay kapansin-pansing umuusad mula sa ibabaw ng bato
Bakit zero ang EMF kapag ang coil ay dumadaan sa eksaktong sentro ng magnet?
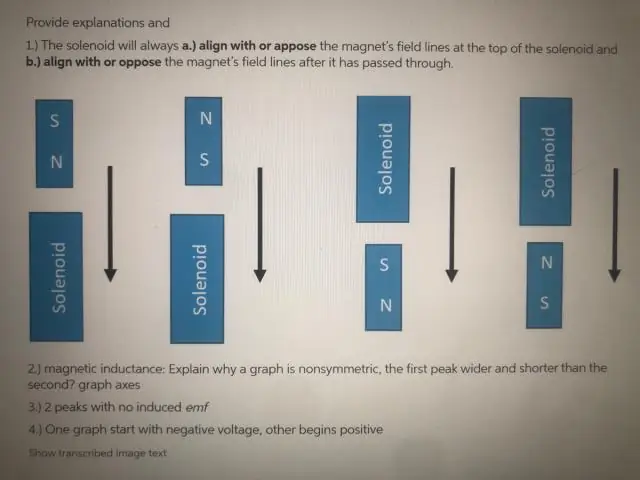
Ang emf ay zero lamang sa isang iglap habang ang magnet ay dumadaan sa eksaktong sentro ng coil. Ito ay dahil ang epekto ng N pole sa isang dulo ng magnet sa dulo ng coil, ay eksaktong kinansela ng epekto ng S pole ng magnet sa kabilang dulo ng coil
Ano ang ginagawang posible ang eksaktong pagtitiklop ng DNA?

Ano ang ginagawang posible ang eksaktong pagtitiklop ng DNA? Ang geometry ng mga indibidwal na pares ng base ay nagbibigay-daan lamang sa isang base na makabuo ng hydrogen bond kasama ang complement base nito
Nalalapat ba ang Michaelis Menten equation sa lahat ng enzymes?

Hindi tulad ng maraming mga enzyme, ang mga allosteric enzyme ay hindi sumusunod sa Michaelis-Menten kinetics. Kaya, ang mga allosteric enzyme ay nagpapakita ng sigmodial curve na ipinakita sa itaas. Ang plot para sa bilis ng reaksyon, vo, kumpara sa konsentrasyon ng substrate ay hindi nagpapakita ng hyperbolic plot na hinulaang gamit ang Michaelis-Menten equation
Aling atomic model ang nagsasabi na imposibleng malaman ang eksaktong lokasyon ng mga electron sa paligid ng nucleus?

Ang sagot ay ang electron-cloud model. Ang modelo ni Erwin Schrodinger, hindi tulad ng iba pang mga modelo, ay nagpapakita ng mga electron bilang bahagi ng isang 'cloud' kung saan ang lahat ng mga electron ay sumasakop sa parehong espasyo nang sabay-sabay
