Video: Ang isang matrix ba ay katulad ng kabaligtaran nito?
2024 May -akda: Miles Stephen | [email protected]. Huling binago: 2023-12-15 23:41
Isipin na lang ang isang 2x2 matris yan ay katulad ng kabaligtaran nito nang hindi 1 o -1 ang mga diagonal na entry. dayagonal matrice gagawin. Kaya, si A at kabaligtaran ng A ay katulad , kaya pareho ang kanilang eigenvalues. kung ang isa sa mga eigenvalues ng A ay n, isang eigenvalues ng kabaligtaran nito ay magiging 1/n.
Tinanong din, ang isang matrix ba ay katulad ng transpose nito?
Anumang parisukat matris sa ibabaw ng isang patlang ay katulad ng transpose nito at anumang square complex matris ay katulad sa isang simetriko complex matris.
Gayundin, magkatulad ba ang lahat ng invertible matrice? Kung ang A at B ay katulad at nababaligtad , pagkatapos ay ang A–1 at B–1 ay katulad . Patunay. Since lahat ang matrice ay nababaligtad , maaari nating kunin ang kabaligtaran ng magkabilang panig: B–1 = (P–1AP)–1 = P–1A–1(P–1)–1 = P–1A–1P, kaya ang A–1 at B–1 ay katulad . Kung ang A at B ay katulad , gayundin ang Ak at Bk para sa anumang k = 1, 2,.
Tungkol dito, maaari bang maging katulad ang isang matrix sa sarili nito?
Ibig sabihin, Any matris ay katulad sa sarili : I−1AI=A. Kung si A ay katulad sa B, pagkatapos B ay katulad sa A: kung B=P−1AP, pagkatapos ay A=PBP−1=(P−1)−1BP−1. Kung si A ay katulad sa B sa pamamagitan ng B=P−1AP, at ang C ay katulad sa B sa pamamagitan ng C=Q−1BQ, pagkatapos ay ang A ay katulad hanggang C: C=Q−1P−1APQ=(PQ)−1APQ.
Ano ang ibig sabihin kung magkatulad ang mga matrice?
Sa linear algebra, dalawang n-by-n matrice A at B ay tinatawag katulad kung mayroong isang invertible n-by-n matris P ganyan. Mga katulad na matrice kumakatawan sa parehong linear na mapa sa ilalim ng dalawang (posibleng) magkaibang base, na ang P ang pagbabago ng batayan matris.
Inirerekumendang:
Paano mo mahahanap ang kabaligtaran ng isang tatsulok gamit ang Pythagorean?
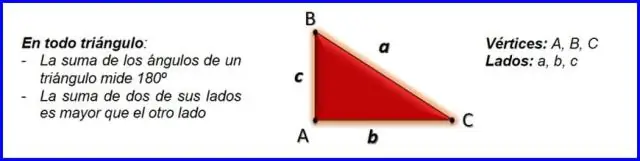
Mga Right Triangles at ang Pythagorean Theorem Ang Pythagorean Theorem, a2+b2=c2, a 2 + b 2 = c 2, ay maaaring gamitin upang mahanap ang haba ng alinmang gilid ng right triangle. Ang gilid sa tapat ng tamang anggulo ay tinatawag na hypotenuse (side c sa figure)
Paano mo gagawing identity matrix ang isang matrix?
VIDEO Bukod dito, paano mo mahahanap ang kabaligtaran ng isang matrix gamit ang isang identity matrix? Gumagana ito sa parehong paraan para sa matrice . Kung magpaparami ka a matris (tulad ng A) at nito kabaligtaran (sa kasong ito, A – 1 ), makuha mo ang matris ng pagkakakilanlan I.
Ano ang kabaligtaran ng kabaligtaran ng - 12?
Ang kabaligtaran ng 12 ay 12, o isang kredito na $12
Ano ang hitsura ng DNA na nauugnay ang kemikal na istraktura nito sa hitsura nito kapag maraming mga ito ay pinagsama-sama?
Iugnay ang kemikal na istraktura nito sa hitsura nito kapag marami sa mga ito ay pinagsama-sama. Ang DNA ay mukhang spider webs. Ang DNA ay natutunaw sa DNA extraction buffer kaya hindi namin ito makita. Kapag hinalo ito sa ethanol, nagkumpol ito at bumuo ng mas makapal at mas makapal na mga hibla na sapat na malaki upang makita
Ano ang flux sa isang cube ng gilid kung ang isang point charge ng Q ay nasa isang sulok nito?
Gaya ng alam natin na, Ang kabuuang pagkilos ng bagay mula sa isang singil q ay q/ε0 (batas ni Gauss). Kung ang charge ay nasa sulok ng isang cube, ang ilan sa flux ay pumapasok sa cube at umaalis sa ilan sa mga mukha nito. Ngunit ang ilan sa flux ay hindi pumapasok sa cube. Ang 1/8th na ito ay hahatiin muli sa 3 bahagi